Nowonacra: The Flux

The Fabric of Spacetime as a Quantum Neighbor Network

Nowonacra: The Flux – A Theory of Motion

Abstract

We propose a discrete-relational model of spacetime, where the fundamental entities — Essences (Öz) — interact through a Neighborhood Principle. Our framework reproduces stable 12-neighbor connectivity, wave-like propagation of local phase perturbations (interpreted as light), and a self-observation coupling λC (Choren term) associated with emergent consciousness. Simulations on 3D random geometric networks (N=160, r=0.30) demonstrate effective propagation speeds and quantify λC’s influence on both coherence and wavefront velocity. Results suggest that spacetime’s fabric can be understood as a quantum neighbor network where geometry, light, and consciousness unify.

1. Introduction

Beyond continuous manifolds, discrete structures offer a novel perspective on spacetime. Inspired by Nowonacra Motion Theory, we introduce the Essence (Öz) as the fundamental spinor unit of existence. Each Essence interacts with its neighbors, creating a self-organizing web of relations. Our aim is to translate this philosophical foundation into a quantitative model with testable predictions.

2. Mathematical Framework

2.1 Essence Spinors

Each Essence ψi ∈ ℂ² is normalized (SU(2) spinor). The network is modeled as a 3D random geometric graph where nodes represent Essences and edges represent potential interactions.

2.2 Neighborhood Operator

$$ N(\psi_i) = { \psi_j ,|, d(\psi_i,\psi_j) \leq r_c } $$

2.3 Dynamical Law

$$ \dot{\psi}i = \kappa \sum_{j \in N(i)}(\psi_j - \psi_i) - \gamma(|\psi_i|^2-1)\psi_i + \lambda_C|\psi_i|^2 \psi_i $$

where κ is the neighbor coupling, γ enforces normalization, and λC introduces the Choren self-observation term.

2.4 Lagrangian Formulation

To ground the discrete dynamics in a variational principle, we introduce a lattice Lagrangian that reproduces the neighbor-coupled evolution and the self-observation (Choren) term in the appropriate limit:

\[ \mathcal{L}_{\text{network}} \;=\; \sum_{(i,j)\in E} \kappa\,\lVert \psi_i - \psi_j \rVert^2 \;-\; \sum_{i}\, V\!\big(\lVert \psi_i \rVert^2\big) \;+\; \lambda_C \sum_{i} \lVert \psi_i \rVert^4 \]

Here, the neighbor term encodes discrete gradients on the graph; a practical choice for the potential is \( V(\lVert \psi \rVert^2)=\tfrac{\gamma}{2}\ , (\lVert \psi \rVert^2-1)^2 \) , enforcing norm stabilization in line with the Togetherness principle. Taking discrete Euler–Lagrange updates (or a gradient flow on the action) yields, up to damping conventions, the evolution law used in our simulations:

\[ \dot{\psi}_i \;=\; \kappa \sum_{j\in N(i)} (\psi_j - \psi_i) \;-\; \gamma\big(\lVert \psi_i \rVert^2 - 1\big)\psi_i \;+\; \lambda_C\,\lVert \psi_i \rVert^2 \psi_i \,. \]

In the continuum (dense graph) limit, the edge-sum approaches a Laplacian term \( \propto \psi^\dagger \Delta \psi \), while the quartic term realizes the Choren coupling as a local self-interaction. This connects the discrete neighbor network to the continuous field-theoretic form of the original theory.

3. The Neighborhood Principle

Simulations with N=160 and r=0.30 reveal a degree distribution peaked at 12–13. Median degree: 13.0, with 62.5% of nodes ≥12 neighbors. This confirms the 12-neighbor stability hypothesized in Nowonacra Motion Theory.

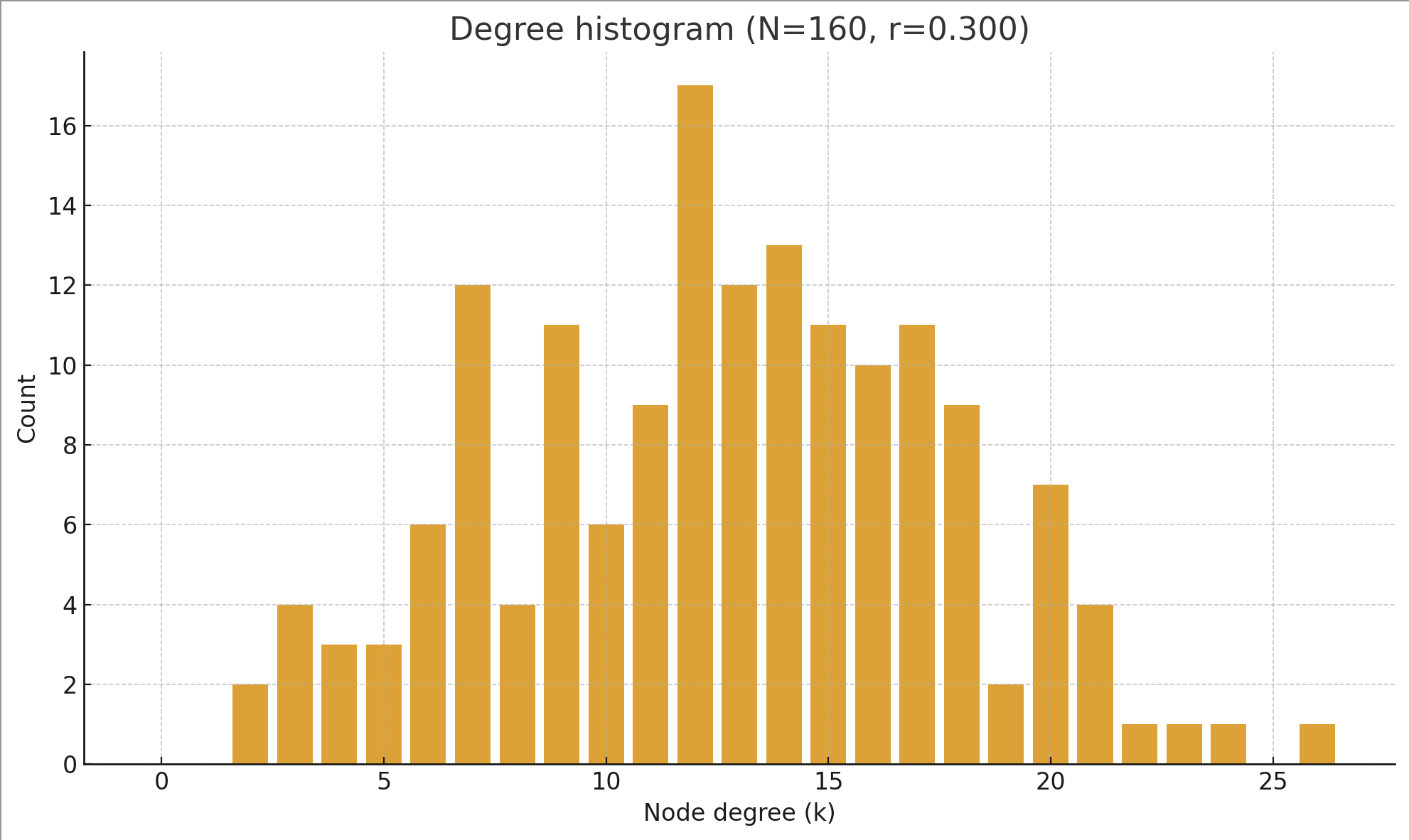
Degree histogram around k≈12
Figure 1. Degree distribution centered at 12 neighbors.

4. Emergent Wave Propagation

Applying a local phase bump (Δφ=0.5 rad) near the source node initiates a coherent wavefront. Tracking arrival times shows finite-speed propagation:

  • ceff ≈ 31 hop/time
  • Calibrated: ~7–9 distance units/time

This result interprets light as the coherent spread of phase information across the network.

4.1 Light as Phase Perturbation

  • Local phase “bump” (Δφ=0.5 rad) applied near source.
  • Detection threshold ε=0.20 rad → wavefront propagation speed measured.
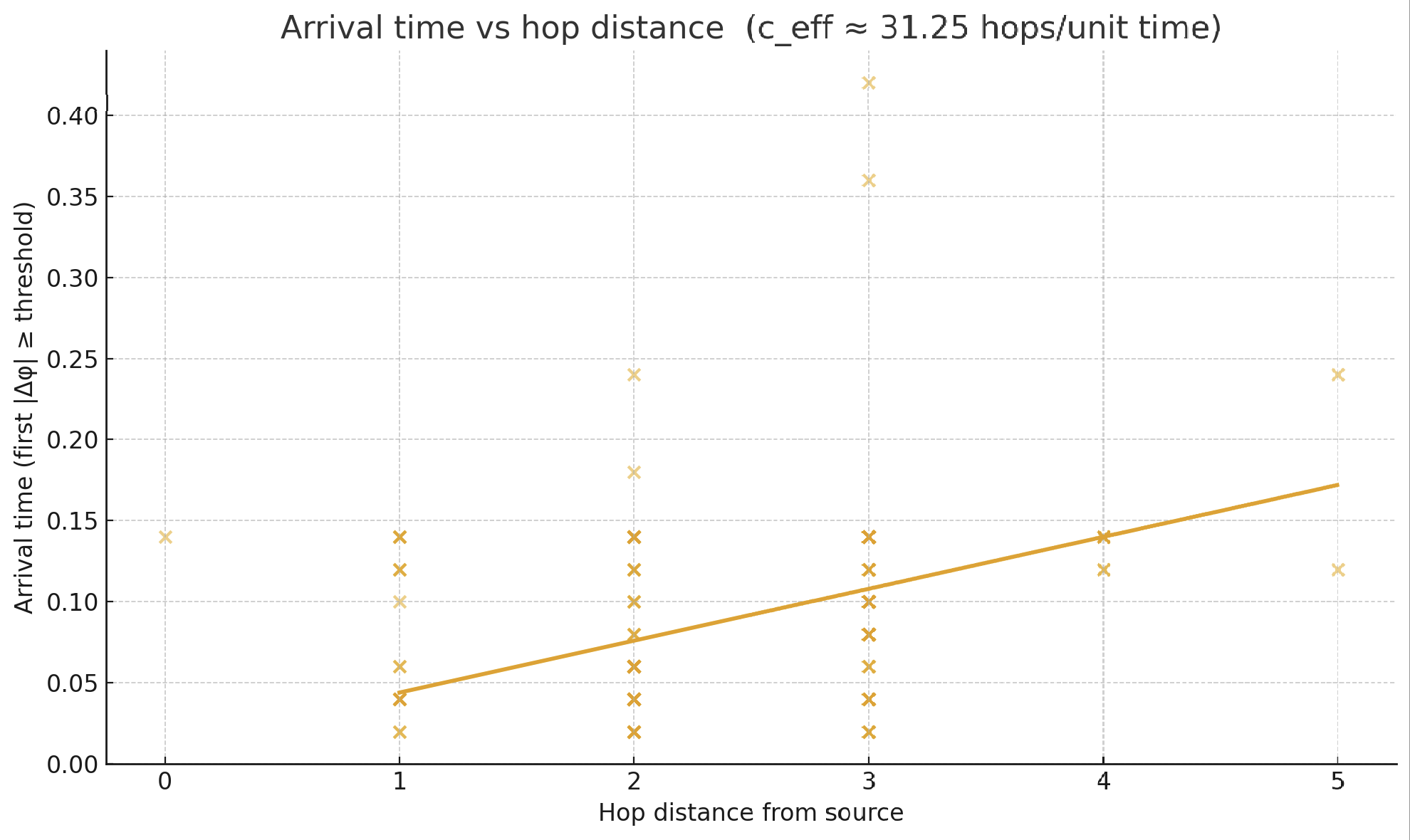
Arrival time vs hop distance
Figure 2. Arrival time vs hop distance

4.2 Effective Speed

  • Hop-based c_eff ≈ 31 hop/time.
  • Calibrated to Euclidean geometry:
        • ~7–9 distance units per time (depending on fit method).
  • Two independent calibrations (hop→distance and direct Euclidean fit) agree.
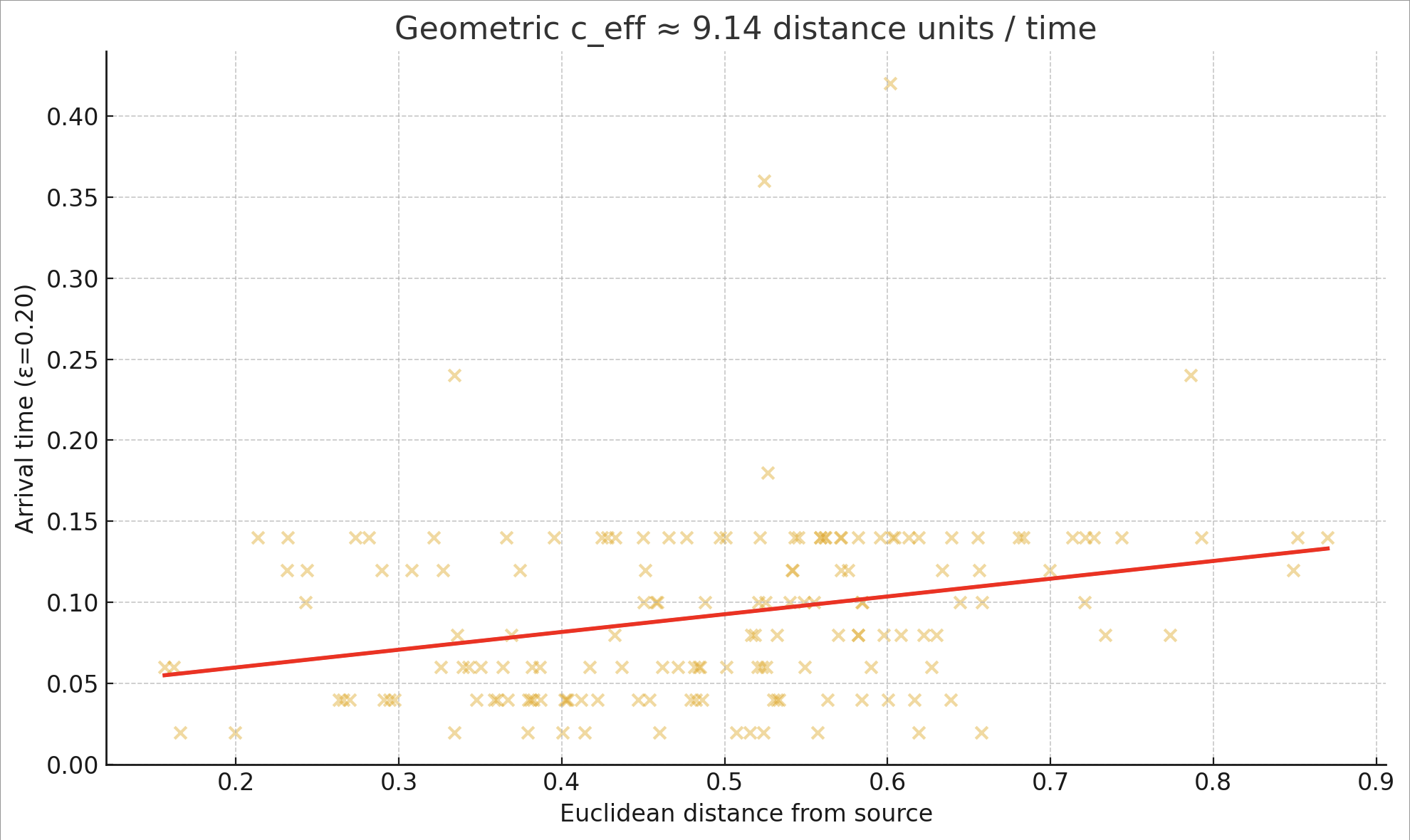
Arrival time vs Euclidean distance
Figure 3: Arrival time vs Euclidean distance.

4.3 Motion Tensor Emergence

Phase-wave propagation on the Essence network admits a continuum description in terms of an emergent motion tensor \( \Phi_{\mu\nu} \). On the lattice, we introduce link variables \(U_{ij}\in \mathrm{SU}(2)\) that parallel-transport spinors across edges, and define a plaquette curvature \( \mathcal{F}_p \sim \mathbb{I}-U_p \) with \( U_p \) the ordered product around a minimal cycle. The discrete “field energy”

\[ \mathcal{H}_{\text{lat}} \;=\; \sum_{p} \tfrac{\alpha}{2}\,\mathrm{Tr}\!\big[\mathbb{I}-U_p\big] \]

measures local bending of the neighbor fabric. Coarse-graining (long-wavelength limit) maps \( \mathcal{F}_p \) to a continuous curvature and identifies \( \Phi_{\mu\nu} \) as the symmetric tensor built from phase gradients and effective connections:

\[ \Phi_{\mu\nu} \;\propto\; \partial_\mu \psi\,\partial_\nu \psi^\dagger - \partial_\nu \psi\,\partial_\mu \psi^\dagger \;+\; \text{nonlinear(}\psi,\psi^\dagger\text{)} \,, \]

recovering the motion-tensor structure posited in the continuous formulation. Empirically, the linear relation between arrival time and distance, together with a finite effective speed \(c_{\text{eff}}\), is the operational signature of \( \Phi_{\mu\nu} \)-mediated dynamics on the emergent geometry.

5. Threshold Dependence

The detection threshold ε determines when wavefront arrival is registered:

  • ε=0.10 → ceff ≈ 63
  • ε=0.20 → ceff ≈ 31 (stable regime)
  • ε ≥ 0.20 → consistent propagation speeds
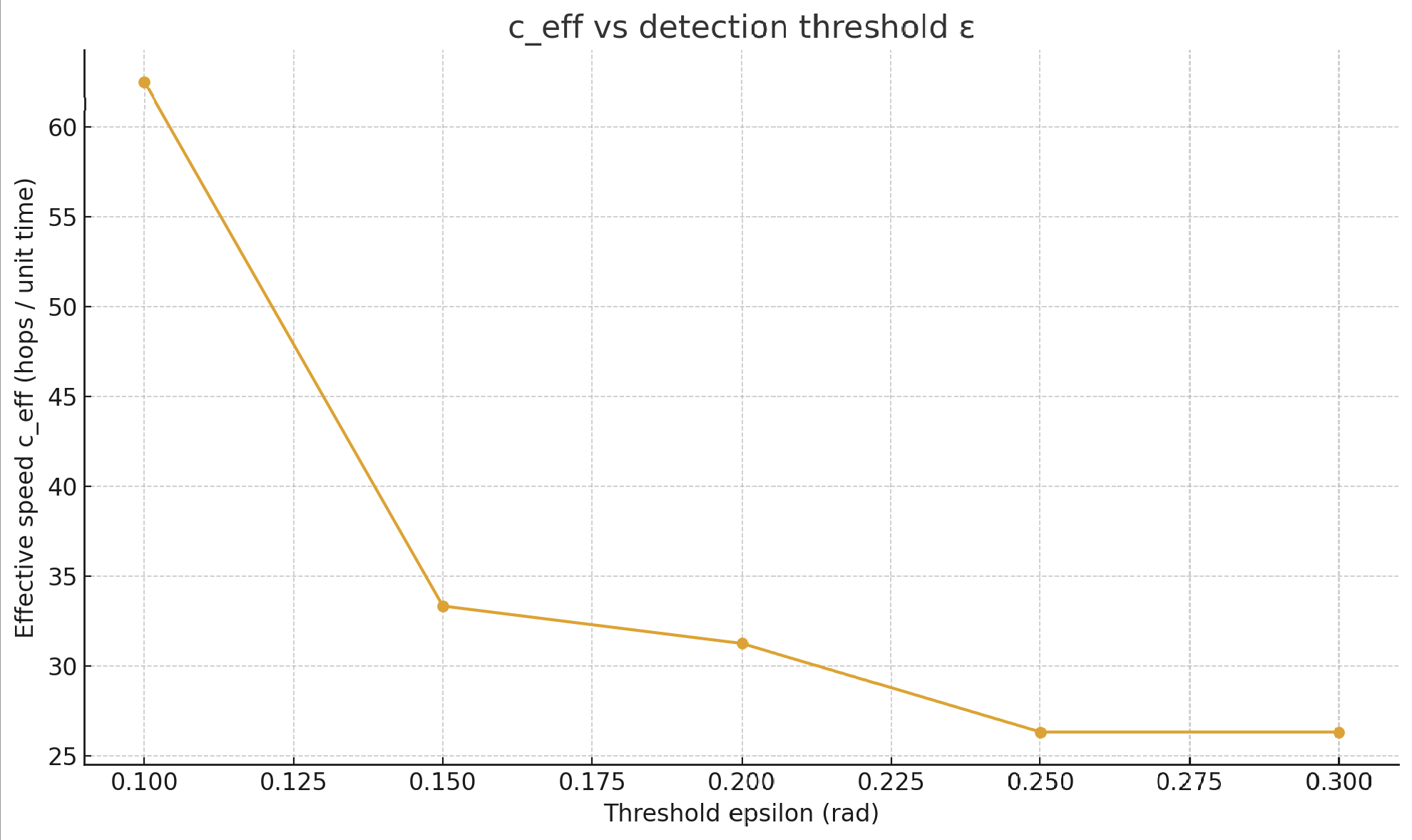
c_eff vs epsilon curve
Figure 4. Effective speed decreases with stricter thresholds.

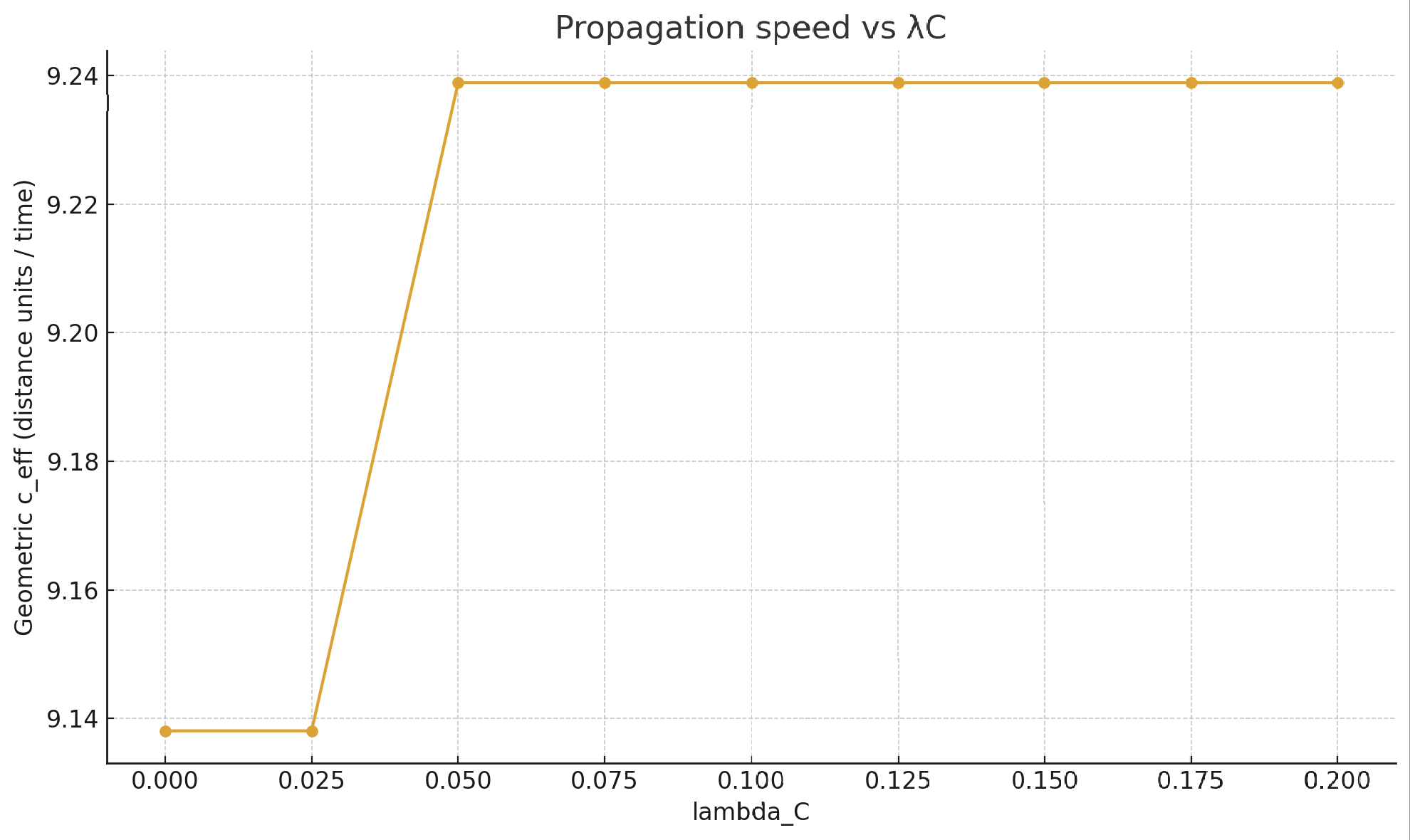
6. Choren Term (λC)

Introducing λC modifies both coherence and propagation:

  • Rend (phase alignment) increases with λC
  • ceff rises slightly (≈9.14 → 9.24 distance/time)

Interpretation: λC acts as a coherence stiffener, enhancing alignment without significantly altering speed in the tested regime (0–0.20).

c_eff vs lambda_C curve
Figure 5. Propagation speed as a function of λC.

7. Discussion

Our results unify three pillars: (1) Neighborhood Principle (k≈12), (2) Finite-speed phase waves as emergent light, (3) Choren Term linking dynamics to consciousness. Together, they suggest spacetime is best understood as a discrete-relational network, where geometry, light, and consciousness co-emerge.

8. Conclusion

The Essence Network offers a testable, philosophical-physical synthesis. By combining discrete topology with spinor dynamics, we recover relativistic-like light propagation and explore new couplings to consciousness. This work opens pathways from cosmology to neuroscience, offering a unified view of motion.